Math Intuition

Under construction

Mathematics

Updated mental models

Numbers aren’t just a count; a better viewpoint is a position on a line. This position can be negative ($-1$), between other numbers ($\sqrt{2}$), or in another dimension ($i$).

Arithmetic became a general way to transform a number. Addition is sliding along the number line ($+3$ means slide 3 to the right) and multiplication is scaling ( $\times 3$ means scale it up 3 times).

Mathematically, the exponent function does this:

$$\mathrm{original}\times {\mathrm{growth}}^{\mathrm{duration}}=\mathrm{new}$$

or $${\mathrm{growth}}^{\mathrm{duration}}=\frac{\mathrm{new}}{\mathrm{original}}$$

Operation	Old concept	New concept
Addition	Repeated counting	Sliding
Multiplication	Repeated addition	Scaling
Exponents	Repeated multiplication	Growth for amount of time

Understanding $e$ (it’s about growth)

The number $e$ is the base amount of growth shared by all continually growing processes. The number $e$ merges Rate and Time. When we write:

$$e^x$$

The variable $x$ is actually a combination of rate and time.

$$x=\text{rate}\times \text{time}$$

So, our general formula becomes:

$$\text{growth}=e^x=e^{rt}$$

The number $e$ is about continuous growth. Intuitively, $e^x$ means:

• How much growth do I get after after $x$ units of time (and 100% continuous growth)

100% continuous growth means that, at any given time, the rate of change is always equal to our current value. Or more mathy: (d/dx)*(e^x) = e^x

Understanding $ln()$ (it’s about time)

• $e^x$ lets us plug in time and get growth.
• $ln(x)$ lets us plug in growth and get the time it would take.

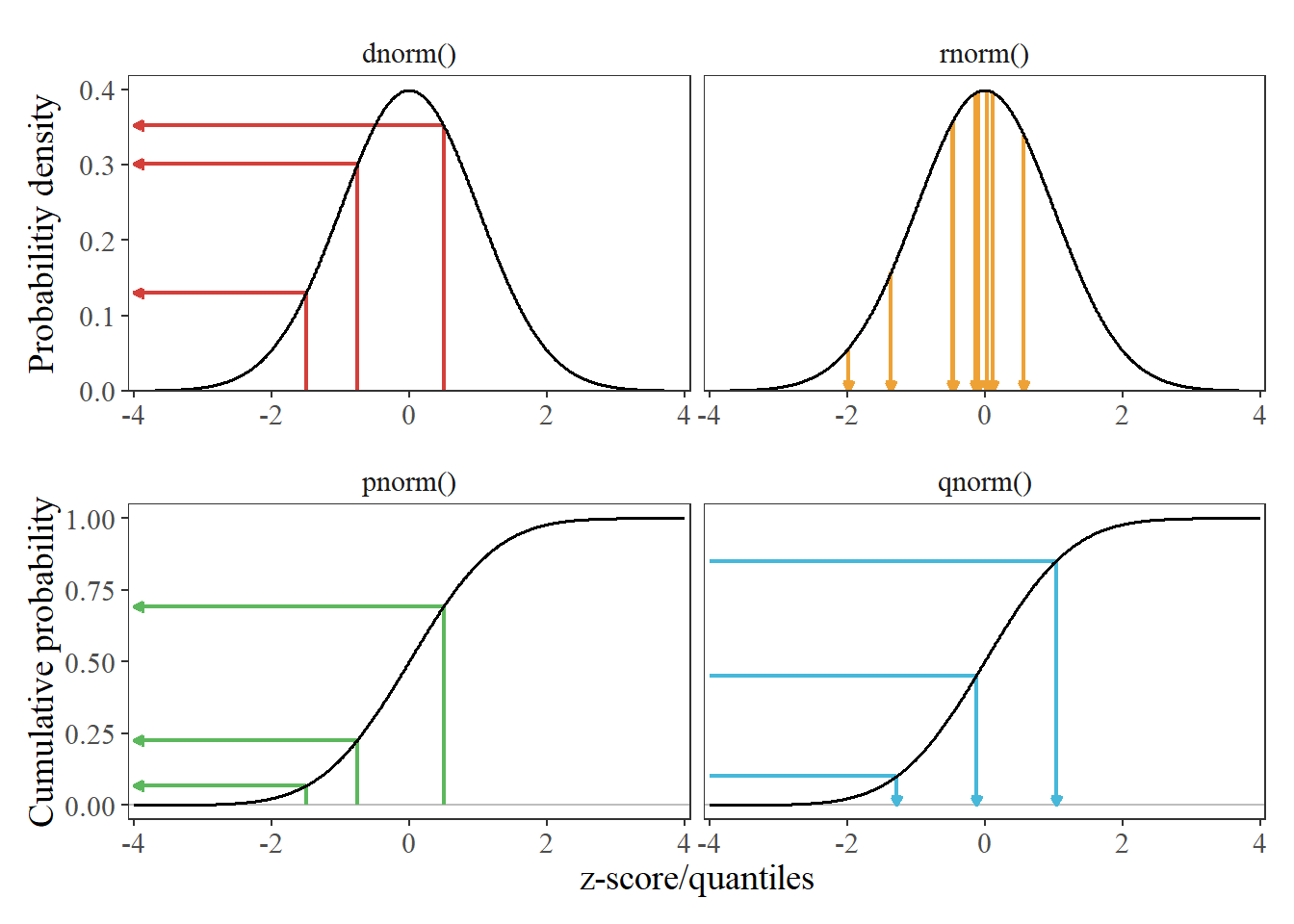
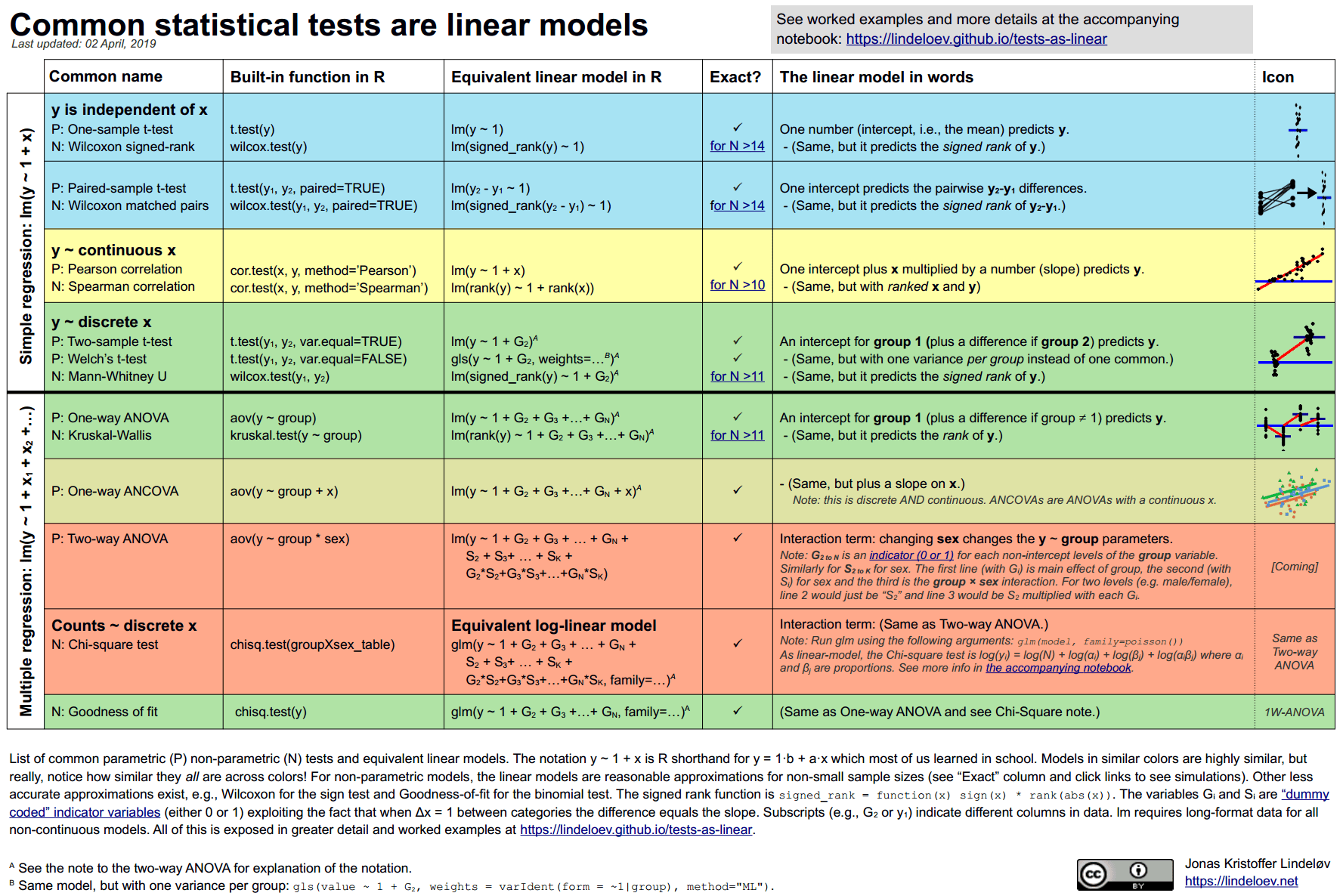
Statistics

• Probability is starting with an animal, and figuring out what footprints it will make.
• Statistics is seeing a footprint, and guessing the animal.

https://wetlandscapes.com/blog/a-brief-visualization-of-rs-distribution-functions/

Common statistical tests are linear models

https://lindeloev.github.io/tests-as-linear/